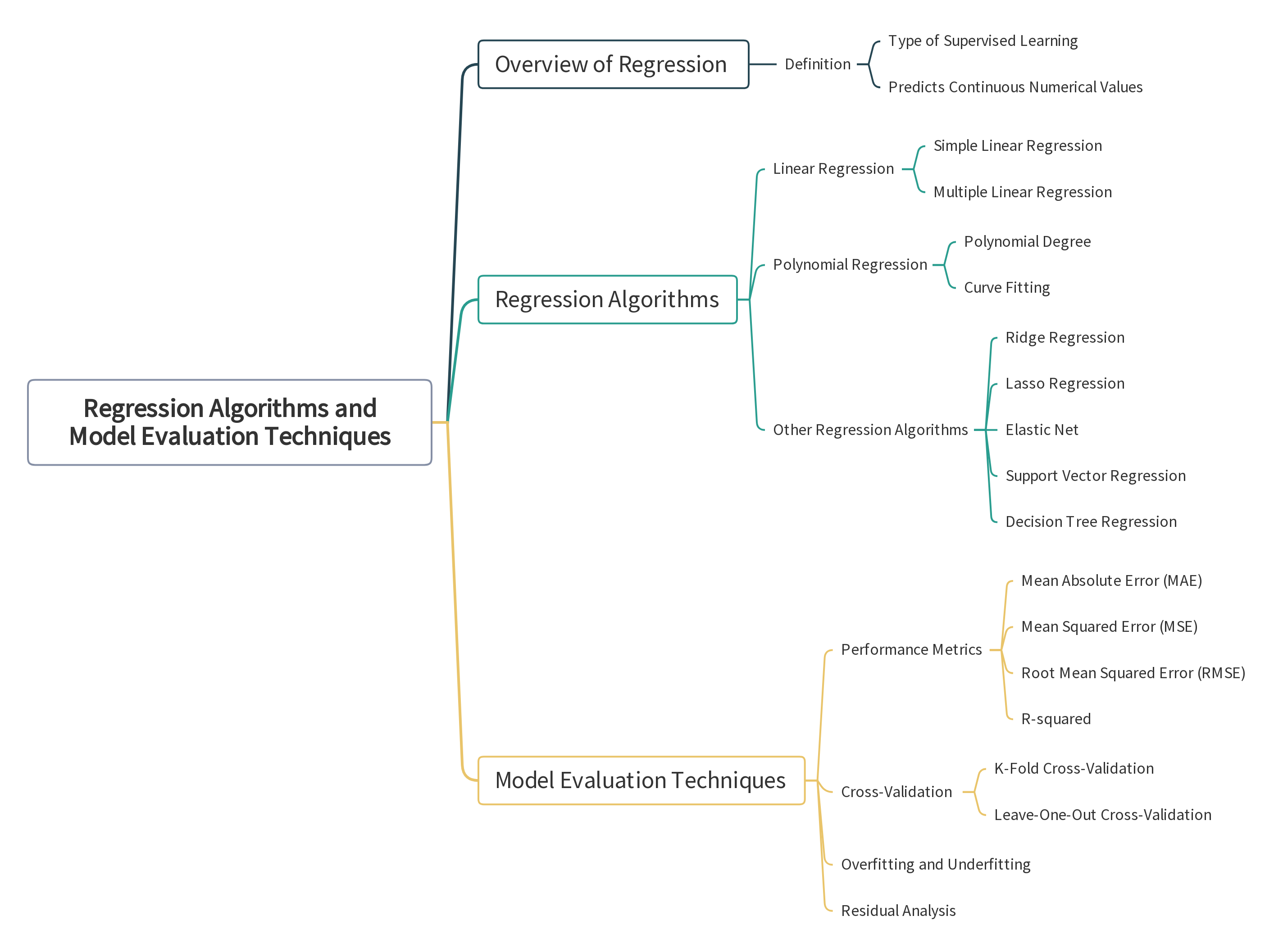
In this section, we will focus on regression algorithms and model evaluation techniques. Regression is a type of supervised learning used to predict continuous numerical values. We will cover several regression algorithms, including Linear Regression and Polynomial Regression. Additionally, we will discuss model evaluation metrics and techniques to ensure the reliability and accuracy of our models. Let's get started!

1. Introduction to Regression

Regression analysis involves predicting a continuous output variable based on one or more input features. It is commonly used in finance, economics, and the natural and social sciences to model relationships between variables.

Example:
Consider a scenario where you want to predict house prices based on features such as square footage, number of bedrooms, and location.

2. Linear Regression

Linear Regression is one of the simplest and most widely used regression algorithms. It models the relationship between the dependent variable and one or more independent variables by fitting a linear equation to the observed data.

Practical Exercise:
Let's build a Linear Regression model to predict house prices based on square footage.

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score

# Load the dataset
data = pd.read_csv('house_prices.csv')

# Split the dataset into features and target variable
X = data[['square_footage']]
y = data['price']

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create a Linear Regression model
model = LinearRegression()

# Train the model
model.fit(X_train, y_train)

# Make predictions
predictions = model.predict(X_test)

# Evaluate the model
mae = mean_absolute_error(y_test, predictions)
mse = mean_squared_error(y_test, predictions)
r2 = r2_score(y_test, predictions)
print(f'MAE: {mae}, MSE: {mse}, R2: {r2}')
    

3. Polynomial Regression

Polynomial Regression extends Linear Regression by allowing for a polynomial relationship between the independent and dependent variables. It is useful for modeling non-linear relationships.

Practical Exercise:
Let's build a Polynomial Regression model to predict house prices based on square footage.

from sklearn.preprocessing import PolynomialFeatures

# Create polynomial features
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X_poly, y, test_size=0.2, random_state=42)

# Create a Linear Regression model
model = LinearRegression()

# Train the model
model.fit(X_train, y_train)

# Make predictions
predictions = model.predict(X_test)

# Evaluate the model
mae = mean_absolute_error(y_test, predictions)
mse = mean_squared_error(y_test, predictions)
r2 = r2_score(y_test, predictions)
print(f'MAE: {mae}, MSE: {mse}, R2: {r2}')

4. Model Evaluation and Validation

Evaluating and validating your machine learning model is crucial to ensure its performance and generalizability. We will discuss various metrics for classification and regression, as well as techniques like cross-validation.

Metrics for Classification:

• Accuracy: The proportion of correctly classified instances.
• Precision, Recall, and F1 Score: Metrics to evaluate the performance of classification models, especially with imbalanced datasets.

Metrics for Regression:

• Mean Absolute Error (MAE): The average of absolute differences between predicted and actual values.
• Mean Squared Error (MSE): The average of squared differences between predicted and actual values.
• R-squared (R2): A statistical measure that indicates the proportion of the variance in the dependent variable that is predictable from the independent variables.

Practical Exercise:
Let's use cross-validation to evaluate our Linear Regression model.

from sklearn.model_selection import cross_val_score

# Perform cross-validation
scores = cross_val_score(model, X_poly, y, cv=5, scoring='neg_mean_squared_error')

# Convert scores to positive values
mse_scores = -scores
print(f'Cross-validated MSE scores: {mse_scores}')
print(f'Mean MSE: {mse_scores.mean()}')

Summary

In this section, we explored regression algorithms, including Linear Regression and Polynomial Regression. We also covered important model evaluation metrics and techniques, such as MAE, MSE, R-squared, and cross-validation. These tools are essential for building reliable and accurate machine learning models.

Stay tuned for the next section, where we will cover practical applications and projects to consolidate your learning. Happy learning!